Here are some more examples that will help understanding the Chapter 5 of the Book, Functional Programming in Scala.
Full source code is here
Introduction
See this code.
List(1, 2, 3, 4).map(_ + 10).filter(_ % 2 == 0).map(_ * 3)
It will be evaulatee in following sequence:
List(1, 2, 3, 4).map(_ + 10).filter(_ % 2 == 0).map(_ * 3)
List(11, 12, 13, 14).filter(_ % 2 == 0).map(_ * 3)
List(12, 14).map(_ * 3)
List(36, 42)
As illustrated below, at each evaluation step, entire data is processed and staged in memory.
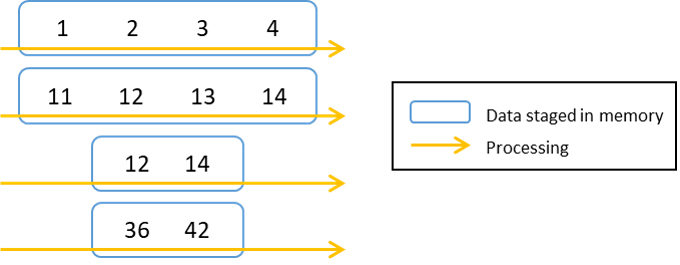
This evaulation style is infeasible or inefficient when:
- Original data is very big.
- All you need is the first element of the result.
So. How about this evaluate style (illustration).
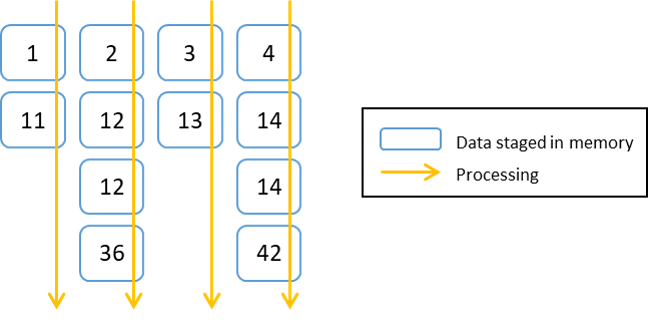
In this style, data is staged in memory just before its processing and can be immediately unstaged after the processing. Those two problems are resolved.
As you may notice now, this can be called the lazy evaluation style. The former one is the strict style.
Today’s question is how to accomplish the lazy style.
Control of Argument Evaluation
We defined a function to test evaluation time.
def time: Long = System.nanoTime
Here’re three functions that demonstrates different methods of passing arguments in Scala.
def callByValue(t: Long) = (t, t, t)
// call by zero-argument function, i.e. thunk
def callByThunk(t: () => Long) = (t(), t(), t())
def callByName(t: => Long) = (t, t, t)
If you execute following:
callByValue(time)
callByThunk(() => time)
callByName(time)
The result is like this:
callByValue: callByValue[](val t: Long) => (Long, Long, Long)
res6: (Long, Long, Long) = (1496801037699293,1496801037699293,1496801037699293)
callByThunk: callByThunk[](val t: () => Long) => (Long, Long, Long)
res7: (Long, Long, Long) = (1496801041075067,1496801041076569,1496801041076870)
callByName: callByName[](val t: => Long) => (Long, Long, Long)
res8: (Long, Long, Long) = (1496801042994466,1496801042995667,1496801042995968)
See the difference?
In callByThunk and callByName, arguments are not evaluated at call time.
In addition to those three evaluation methods, Scala offers lazy variable. When a variable is defined lazy, it is evaluated at the first time it is accessed. And from then on, it is staged in memory. When you execute following code:
lazy val time2: Long = System.nanoTime
callByValue(time2)
callByThunk(() => time2)
callByName(time2)
The result is as follows.
time2: Long = 1496801046125958
res10: (Long, Long, Long) = (1496801046125958,1496801046125958,1496801046125958)
res11: (Long, Long, Long) = (1496801046125958,1496801046125958,1496801046125958)
res12: (Long, Long, Long) = (1496801046125958,1496801046125958,1496801046125958)
The nine value are all equal. This is because the firstly evaluated value is staged in memory and not changed from then on. This behavior of a lazy variable is called memoization.
The Stream data structure
Based on the lazy type variable, we can define a new data structure that will be evaluated in lazy style. In Scala it is called Stream.
sealed trait Stream[+A]
case object Empty extends Stream[Nothing]
case class Cons[+A](h: () => A, t: () => Stream[A]) extends Stream[A]
object Stream {
def cons[A](hd: => A, tl: => Stream[A]): Stream[A] = {
lazy val head = hd // Memoization
lazy val tail = tl // Memoization
Cons(() => head, () => tail)
}
def empty[A]: Stream[A] = Empty
def apply[A](as: A*): Stream[A] =
if (as.isEmpty) empty
else cons(as.head, apply(as.tail: _*))
def map[B](f: A => B): Stream[B] = s match {
case Cons(h, t) => cons(f(h()), t().map(f))
case _ => empty
}
def filter(p: A => Boolean): Stream[A] = s match {
case Cons(h1, t1) if p(h1()) => cons(h1(), t1().filter(p))
case Cons(_, t2) => t2().filter(p)
case _ => empty
}
def toList: List[A] = s match {
case Empty => Nil
case Cons(h, t) => h() :: t().toList
}
}
Although it seems complex, all you need to remember is this single figure:

The key points are:
- To store data in a fold-right chain of binary function
conswhich receives by-name arguments. - To memoize data when it is evaluated (implemented in
consfunction usinglazyvariables).
Evaluation Example
Let’s see the following example. It is little-bit simplified version of the first example above, with the toList method to fire evaluation.
Stream(1, 2, 3, 4).map(_ + 10).filter(_ % 2 == 0).toList
This will be evaluated in lazy style as follows:
Stream(1, 2, 3, 4).map(_ + 10).filter(_ % 2 == 0).toList
cons(11, Stream(2, 3, 4).map(_ + 10)).filter(_ % 2 == 0).toList
Stream(2, 3, 4).map(_ + 10).filter(_ % 2 == 0).toList // filtered
cons(12, Stream(3, 4).map(_ + 10)).filter(_ % 2 == 0).toList
12 :: Stream(3, 4).map(_ + 10).filter(_ % 2 == 0).toList
You can see the evaluation is done element-wise not function-wise. The first and second elements (1 and 2) are fully evaluated and result in 12. The other elements remains untouched. See Stream(3, 4).map(_ + 10).filter(_ % 2 == 0).toList. Here, the remaining elements are primitive integers. But if they were function calls, they would not have been evaluated yet.
We can accept this. But it is too abstract. How exactly it is done? Here’s the unleashed version.
Detailed Evaluation Steps
Stream(1, 2, 3, 4).map(_ + 10).filter(_ % 2 == 0).toList
// Evaluate apply() constructor
cons(1, cons(2, cons(3, cons(4, empty)))).map(_ + 10).filter(_ % 2 == 0).toList
// Evaluate cons
{
lazy val head = 1
lazy val tail = cons(2, cons(3, cons(4, empty)))
Cons(() => head, () => tail)
}.map(_ + 10).filter(_ % 2 == 0).toList
// Evaluate map // case Cons(h, t) => cons(f(h()), t().map(f))
{
lazy val head = 1
lazy val tail = cons(2, cons(3, cons(4, empty)))
cons(head + 10, tail.map(_ + 10))
}.filter(_ % 2 == 0).toList
// Evaluate cons (in the way to evaluate filter)
// Different variable names head2, tail2 are used for convenience
{
lazy val head = 1
lazy val tail = cons(2, cons(3, cons(4, empty)))
{
lazy val head2 = head + 10
lazy val tail2 = tail.map(_ + 10)
Cons(() => head2, () => tail2)
}
}.filter(_ % 2 == 0).toList
// evaluate filter // case Cons(_, t2) => t2().filter(p)
// Note that head, head2 is evaluated in match-case statements of the filter
{
val head = 1 // evaluated !
lazy val tail = cons(2, cons(3, cons(4, empty)))
{
val head2 = head + 10 // evaluated !
lazy val tail2 = tail.map(_ + 10)
tail2.filter(_ % 2 == 0)
}
}.toList
// Simplification (No top-level functions evaluated)
// - head1, head2 are not used (will become not assessible and be removed by garbage collector),
// - redundant braces are flattened/removed,
// - redundant lazy keywords are flattened/removed.
{
lazy val tail = cons(2, cons(3, cons(4, empty)))
{
lazy val tail2 = tail.map(_ + 10)
tail2.filter(_ % 2 == 0)
}
}.toList
// Further simplification
{
{
lazy val tail2 = cons(2, cons(3, cons(4, empty))).map(_ + 10)
tail2.filter(_ % 2 == 0)
}
}.toList
// Further simplification
cons(2, cons(3, cons(4, empty))).map(_ + 10).filter(_ % 2 == 0).toList
See how the first element is processed?
Let’s do it one more time.
// Evaluate cons
{
lazy val head = 2
lazy val tail = cons(3, cons(4, empty))
Cons(() => head, () => tail)
}.map(_ + 10).filter(_ % 2 == 0).toList
// Evaluate map // case Cons(h, t) => cons(f(h()), t().map(f))
{
lazy val head = 2
lazy val tail = cons(3, cons(4, empty))
cons(head + 10, tail.map(_ + 10))
}.filter(_ % 2 == 0).toList
// Evaluate cons (in the way to evaluate filter)
{
lazy val head = 2
lazy val tail = cons(3, cons(4, empty))
{
lazy val head2 = head + 10
lazy val tail2 = tail.map(_ + 10)
Cons(() => head2, () => tail2)
}
}.filter(_ % 2 == 0).toList
// Evaluate filter // case Cons(h1, t1) if p(h1()) => cons(h1(), t1().filter(p))
{
val head = 2 // evaluated !
lazy val tail = cons(3, cons(4, empty))
{
val head2 = head + 10 // evaluated !
lazy val tail2 = tail.map(_ + 10)
cons(head2, tail2.filter(_ % 2 == 0))
}
}.toList
// Simplification
cons(12, cons(3, cons(4, empty)).map(_ + 10).filter(_ % 2 == 0)).toList
// Evaluate cons (in the way to evaluate toList)
{
lazy val head = 12
lazy val tail = cons(3, cons(4, empty)).map(_ + 10).filter(_ % 2 == 0)
Cons(() => head, () => tail)
}.toList
// Evaluate toList // case Cons(h, t) => h() :: t().toList
12 :: cons(3, cons(4, empty)).map(_ + 10).filter(_ % 2 == 0).toList
See how the second element is processed?
Discussion
This is it.
Scala’s lazy evaluation was the key to build Spark. I hope this example help understanding lazy concept.